You are here:

Predicting the spread of the Coronavirus

Editorial Staff

[latexpage]

With over 86,000 people infected and around 3,000 people killed, the new Coronavirus is something to be taken very seriously. The new virus which has been called Covid-19 was discovered in Wuhan, China earlier this year. Not only has it taken a big toll on the Chinese economy, other countries in the world are being affected by the virus as well. In order to tackle the virus, several organisations have volunteered to help China with the fight against the virus. Moreover, several scientists are coming up with models to predict where and when the virus will spread out to. This article will try to explain how predicting the spread of the Coronavirus can be a huge contribution to our world. 

 

Impact on the economy

Before we dive into the models used to explain the behaviour of the Coronavirus, I will first explain what kind of models are used to estimate the economic impact of natural disasters. A study that has been conducted by Sayanti Mukherjee and Makarand Hastak from Purdue University explain what kind of models are used to predict the impact of natural disasters like floods, earthquakes and also epidemics. They used a panel data regression model to determine the significance of various variables and predict the overall impact. As a natural disaster can have an effect on the economy for several years, the data that is being used is a multidimensional dataset that observes series of cross-sectional data over time. To illustrate:

 

7464

Source: Mukherjee and Hastak

 

This figure illustrates how the dataset should be interpreted by the model. The grey first layer is data about every country $1, \dots , n$ that has been struck by a disaster in year $t_1$ and the economic data of the year $t_0$. By using the economic data from an initial year, $t_0$, before a disaster we can actually compare what the impact on the economy will be. The next layer will be the following year $t_2$ for the disaster data and $t_1$ for the economic set and so forth. Eventually we can have an m (years) by n (countries) multidimensional data set. If we only looked at the effects of every country in the year the disaster took place in our dataset we would overlook the effect of time, which can have a big impact. Therefore, we have to have a model that includes both the location and time of all our variables to conduct our analysis.

A very basic econometric model that can be used to predict economic growth with such disasters is as follows:

\begin{equation}
\begin{split}
&  Growth_{i,t} = \eta_i + \phi_t + \delta_i*t + \alpha_{i, t}*Impact_{i, t} + \\
& \beta_{i, t} * EconFactors_{i, t} + \epsilon_{i,t}
\end{split}
\end{equation}

Here the variable $Growth_{i, t}$ is measured as a percentage change in real GDP per capita in time $t$ of country $i$. Moreover, $\eta_i$ is the so called [expand title = “fixed effects”] The $\eta_i$ are entity-specific intercepts that capture heterogeneities across entities. The fixed effects regression model can for example be:  $Y_{it} = \beta_0 + \beta_1X_{it} + \beta_2Z_{i} + \epsilon_{it}$. Where we aim to estimate $\beta_1$, then we let $\eta_i = \beta_0 + \beta_2Z_i$ to obtain the following model: $Y_{it} = \eta_i + \beta_1X_{it} + \epsilon_{it}.$ The $\eta_i$ is then the fixed effects of our model. So basically the fixed effects are factors that do not have an impact over time, but they can have an effect on different countries.[/expand] of a country $i$,  $\phi_t$ is an unobserved time-variant individual effect, which in this case is the global shock over time. The variable “Impact” is, for example, the number of people that have been affected by a disease or have been killed by a flood. The variable “EconFactors” can be variables like population, purchasing power, interest rates or damage costs due to for a flood. At last, for the sake of simplicity, we assume that the [expand title = “zero conditional mean”] The error term $\epsilon_i$ has conditional mean zero given $X_i$ such that $E(\epsilon_i|X_i)=0$.[/expand] assumption holds in this case.

The study  conducted by Mukherjee and Hastak used this model to estimate the effects of various disasters to multiple countries over a time span of several years. Their conclusion was that when a disaster strikes a country, in general, the country suffers from economic growth decrease, but will thrive again after some years. However, a developed country will not necessarily be affected by a decrease in economic growth. Although China can be considered as a developed country, the country is suffering from a big decrease in economic growth, as it has been hit by the virus. As the figure below predicted, China’s economy has a big downfall due to the outbreak of the virus. Furthermore, analysts at Morgan Stanley say that China’s growth could be as low as 3.5% if production levels are not back to normal as soon as possible. So as developed a country may be, a big natural disaster like this can have a big impact on a country’s economy. 

 

7463

Source: Reuters

 

Global risk assessment model

Many people think that the Coronavirus discovered in Wuhan is a whole new disease. However, this is not the case as the Coronavirus is a family of coronaviridae. It consists of 40 different species that have to be treated in a different way. The SARS virus and the MERS virus are also Coronaviruses that had an impact on our world. In 2003 SARS has taken the lives of 774 people and the MERS virus has taken its toll on over 400 people. Even the common cold is a form of a Coronavirus. However, the virus that has now been discovered is much more vigilant than any other Coronavirus that has been known.

So it is very important for policy makers and politicians to know how viruses are being spread. Scientists, in particular Dirk Brockmann at the Royal Koch Institute, have made this spread somewhat clearer using various models to predict where the virus is going to spread in the near future. In particular, they use an import risk model to analyse the behaviour of the disease being transmitted from one country to another. Therefore, the model has to calculate the probability that the disease will go from one airport to another. One can now imagine that this model becomes a very complex network of worldwide airports with probabilities from going from one place to another where the virus could be active. Such a network can be illustrated by this figure:

 

7462

Source: Event Horizon – COVID-19

This figure illustrates the most probable spreading routes from Beijing international airport to every other airport in the world. The size of every node corresponds with the probability that the disease will go there. Moreover, the vertical distance between two nodes is a so called effective distance, which is used to compute the expected arrival times and spreading speeds of the disease.

 

Worldwide air transportation network

To conduct such an analysis like the global risk assessment model, we need a vast amount of data of almost all airports on this planet. Air transportation plays a key role whenever there is a threat for a global pandemic. Therefore, it is extremely important that data at airports is constantly being recorded. Factors such as the connections of an airport, how many times a certain flight route is used, the average amount of passengers per day, the average amount of passengers going to a certain destination, are registered in the dataset. Thus, the core of our model is based on the worldwide air transportation network (WAN).

This is a network that contains 3,893 airports that are connected by 51,476 flight routes. One can imagine that not every route is as popular as the other. Therefore, each route is weighted via a traffic flux, which is simply the average amount of passengers that travel each route on a certain day. After every link has been weighted, we also need to consider the fact that not every airport is as busy as the other. As a consequence, the WAN also has a node flux, which is a measurement of how many people on average traverse an airport on a certain day.

The WAN is dominated by big airports. Even if approximately 2,000 small airports were removed from the network, only 7% of total air traffic would be lost. This is something that has to be taken into consideration when we want to model the risks of a disease spreading to another country. Because big hubs are more likely to be infected by a disease, the smaller hubs will have a significantly smaller probability of becoming infected. However, this does not mean that they should be neglected, because the smaller airports are usually close to the big hubs. Therefore, the disease spreads easily within or between any country, as passengers usually fly to a big airport to subsequently travel to a smaller one. Thus, we will consider every node in the WAN in our model to come up with the best predictions.

 Import risk model

The model that has been used to come up with nice figures as described above are computed with a so called import risk model. This model tries to answer the question: Given the spatial and regional distribution of confirmed cases, what is the likelihood of importing a case from an affected location to an airport or country distant from the outbreak location? This may seem a little complicated to understand, but it basically tries to describe what the probability is that a disease at a given starting point will go to another point in a specific period.

To generalise this let $n_0, \dots , n_N$ be the nodes in our network, where a node can be seen as an airport. We want to model the probability that the disease is imported from the starting node $n_0$ to node $m$. We denote this by: $p(m|n_0)$. In the network used by the scientist of the Royal Koch Institute there are 3893 nodes (airports) and 51,476 links (flight routes), which is simply the same network as the WAN. In order to calculate these probabilities we need a flux matrix $\textbf{F}$. Where the elements $F_{nm}$ denote the passenger traffic from node $m$ to $n$. Notice that $F_{nm} \geq 0$.

Let us now define a path $\Gamma = n_i$, where $i = 0, \dots , L$, as a sequence of $L$ steps along a set of $L + 1$ nodes. Then we have two possibilities for the probability of each possible path. There is a transition probability and an exit probability. The first one is the probability of a person at node $n$ travelling to another node will be node $m$. For example, it is the probability that a person in Wuhan will travel to Amsterdam. This will be denoted by $P_{nm}$. The second one is the probability of a person travelling will exit the system at arrival at node $n$. This will be denoted by $q_n(n|n_0)$, where $0 \leq q_n \leq 1$. Notice that the probability of a person continuing its travels is $1 – q_n$. 

Now having defined our path and transition and exit probabilities, we can now determine the probability of a person travelling a certain path $\Gamma$. For the scope of this article, we assume that we can derive $P_{nm}$ and $q_n$ from our flux matrix $F_{nm}$. We then get the following:

\begin{equation}
p(\Gamma) = q_{n_L}P_{n_{L}n_{L – 1}}(1 – q_{n_{L- 1}}) * \dots * P_{n_1n_0}(1 – q_{n_0})
\end{equation}

Which can be reduced to:
\begin{equation}
p(\Gamma) = q_{n_L}\prod_{k = 1}^LS_{n_kn_{k – 1}}
\end{equation}

Where:

\begin{equation}

S_{nm} = P_{nm}(1 – q_m)

\end{equation}

Also notice that:
\begin{equation}
\sum_{\Gamma \in \Omega}p(\Gamma) = 1
\end{equation}

Hence, the probability that a certain path is taken from the set of all paths denoted by $\Omega$ by a traveller must occur. Now we can determine the probability that a certain person that could have the disease travels to a certain location via a specific path. The other part of the question was when this particular person, who could have the disease, arrives at a certain airport. So we need to add a certain time variable to our model. We can define this time as the number of steps it takes to go from node $n_0$ to node $n_L$, for example. Let this be defined by $\Omega(n_L, n_0, t)$. Then the probability that a person starting at node $n_0$ travels to node $n_L$ via a certain path exits the system at time t is given by:


\begin{equation}
p(n_L, t|n_0) = q_{n_L}\sum_{n_{L – 1}}\sum_{n_{L – 2}} \dots \sum_{n_2}\sum_{n_1}\Big(\prod_{k = 1}^LS_{n_kn_{k – 1}}\Big)
\end{equation}
Which can be reduced to:
\begin{equation}
p(m, t | n_0) = q_m * (\textbf{S})^t_{mn_0}
\end{equation}

Now we finally have all the tools we need to make our model. Notice that the last equation can be interpreted as the probability that someone from China or any other country arrives in Europe or somewhere else at a certain time $t$. If we then use these probabilities to the traffic data and disease locations, we can get an estimate where and when the disease will pop up. Moreover, using minimal spanning tree algorithms will give us these nice figures as shown below.

 

7465

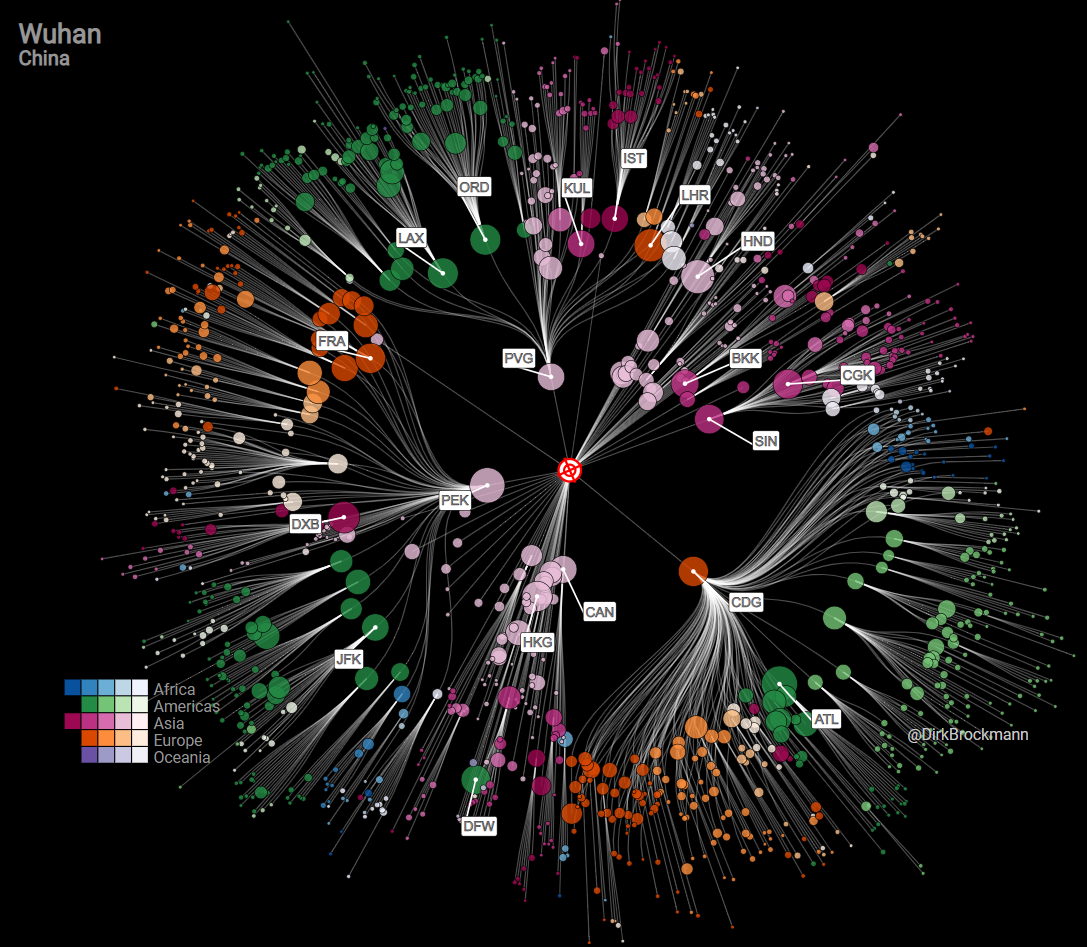
Source: Event Horizon – COVID-19

From this model and the data, the scientists predicted that Taiwan, Hong Kong, South Korea, Japan and Thailand had the most risk of becoming infected. All of these countries have confirmed cases of the new Coronavirus. However, the model predicted that the Netherlands would have a significantly smaller risk of becoming infected. Sadly, there have been reports of the virus in the Netherlands. So even with such a small risk the virus still managed to enter this country. As a consequence, an important lesson should be taken from this event: the model does not predict with absolute certainty when en where the disease will spread, it is only an indication from the data that is available. Furthermore, note that a disease can also spread via trains or cars, which is not considered in this model. However, it is still a very powerful tool to compare the risks of different countries and set an indication of what policy makers should or could do.

Conclusion

We discovered how we can use econometrics, risk modelling and a bit of OR to come up with solutions to predict where and when the Wuhan virus might go to and how it will spread. We have also seen how models can be used to estimate the effects on our economy and what factors may play a big role in such situations. Not only policy makers and politicians can be affected by these predictions, it also gives us a better understanding on how to deal with such extreme situations and prepare us for what may come next. That is simply the power of data and econometrics.

References

This article is written by Sam Ansari

6756