[latexpage]
One of the most popular regression methods an econometrician learns is the Ordinary Least Squares (OLS). It is a simple and elegant way of estimating parameters in linear regression. However, there is another technique to perform linear regression using concepts from machine learning. This concept is called gradient boosting and is also related to decision trees.
Decision trees
A decision tree uses a tree-like model of decisions and possible consequences. It is a very common data mining algorithm used for operations research, specifically in decision analysis. The idea behind it can easily be understood with a small example. Suppose we want to decide whether to take the bus or walk to a certain destination depending on certain parameters. These parameters could include: what the weather is like, how much time it takes to get there or whether you are hungry. Then a simple decision tree can be made as is shown in the figure below.

Example of a decision tree
Decision trees are also used for machine learning principles. This is called decision tree learning and it is a method commonly used in data mining. The goal is to create a model that predicts the value of a target variable based on several input variables. In our example, the target variable is whether to take the bus or walk and the input variables are the weather, the amount of time and whether we are hungry or not. The yellowish squares at the end of the decision tree are called leaves. These decision trees will be used when we will talk about gradient boosting.
Moreover, decision trees can already actually be of really good use. This is due to the fact that these trees are simple to construct and understand. However, there are some limitations to the usage of these trees. For example, decision trees can be non-robust, meaning that a small change in the training data set can result in a significant change in the final prediction or the tree itself. A solution to this is to use multiple decision trees, which is an ensemble method. If you want to learn more about ensemble methods I mention them in one of my previous articles about machine learning in financial markets. Moreover, the ensemble method of using multiple decision trees is used in many boosting methods such as gradient boosting which is explained in the following section.
Gradient boosting
Gradient boosting for regression was developed in 1999 by Jerome H. Friedman. Like other boosting methods, boosting can be interpreted as an optimization algorithm on a suitable cost or loss function. The word gradient is used here because we will use the derivative of the loss function for optimization. So you may wonder why I was talking about decision trees before. This is simply because it is very common that gradient boosting is used with decision trees. This will become more clear when explaining the algorithm.
It is easiest to explain this in the least-squares regression setting, where we have a model $F$ that we want to “teach” to predict the values $\hat{y} = F(x)$ by minimizing the mean squared error ([expand title= MSE] The general formula for this is: $\frac{1}{n}\sum_{i=1}^n(y_i – \hat{y}_i)^2$, where $\hat{y}_i$ is the predicted value and $y_i$ is the observed value. [/expand]). Here $x$ is simply the explanatory variables in our model. Now we want to “boost” this procedure with an algorithm that includes $M$ stages. At each stage $m$ ($1 \leq m \leq M$) suppose we have an imperfect model $F_m(x)$ which we want to improve. This can be done by adding a new estimator to the model as such:
\begin{equation}
F_{m+1}(x) = F_m(x) + h_m(x) = y.
\end{equation}
Or equivalently,
\begin{equation}
h_m(x) = y – F_m(x).
\end{equation}
So gradient boosting will actually fit $h$ to the residual of the regression at each stage, where each $F_{m+1}(x)$ attempts to correct the errors of its predecessor $F_m(x)$.
As mentioned earlier, the algorithm in least-squares setting tries to minimize the MSE at each stage of the learning process, which means that the loss function in our context is actually the MSE itself. There are other loss functions that could be used, but for the sake of simplicity, we will stick to this function. So we define our loss function to be:
\begin{equation}
L(y, F(x)) = \frac{1}{2}(y – \hat{y})^2.
\end{equation}
The factor $\frac{1}{2}$ is used to make computations simpler. With this we have our input of the algorithm assuming we have a training data set ${(x_i,y_i)}_{i=1}^n$.
Moving on to the first step of the algorithm, we must initialize a model with a constant value, which will look like the following:
\begin{equation}
F_0(x) = \underset{\gamma}{\text{argmin}}\sum_{i=1}^nL(y_i, \gamma),
\end{equation}
where $\gamma$ is simply the predicted value of our base model. The first step simply means that we need to find a $\gamma$ that minimizes the loss function. So plugging in our loss function we would get:
\begin{equation}
\begin{split}
\underset{\gamma}{\text{argmin}}\sum_{i=1}^n\frac{1}{2}(y_i – \gamma)^2 \\
\Longrightarrow \frac{d}{d\gamma} \sum_{i=1}^n\frac{1}{2}(y_i – \gamma)^2 = 0 \\
\Longrightarrow -\sum_{i = 1}^ny_i + n\gamma = 0 \\
\Longrightarrow \gamma = \frac{1}{n}\sum_{i = 1}^n y_i = \Bar{y}.
\end{split}
\end{equation}
That means that our initial predicted value is simply the sample average.
Now we will move on to step 2, where the decision trees will be introduced. We will first calculate the so-called pseudo residuals with the general formula:
\begin{equation}
r_{im} = -\left[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]_{F(x) = F_{m-1}(x_i)} \text{for $i = 1, \dots ,n$}.
\end{equation}
This looks like a nasty formula, but it is actually something we already calculated. We take the derivative of the loss function with respect to the predicted value and fill in the predicted value of the previous iteration, which is $-(y_i – \gamma) = -(y_i – F_{m – 1}(x))$. Note that this is only the case for a loss function that is the MSE. Furthermore, we have that $\gamma = \Bar{y}$ for $m = 1$, which is the initial predicted value. Thus, $r_{im}$ is simply equal to $y_i – F_{m-1}(x)$, as we had a minus sign in front of the derivative in the equation for $r_{im}$. Now we have found the residuals, we must fit a regression tree to the $r_{im}$ values and create terminal regions $R_{jm}$, for $j = 1, \dots , J_m$, where $J_m$ is the number of leaves the tree has. This is illustrated in the figure below. We see that for the small data set, the residuals for each observation have been calculated and that a regression tree is constructed based on these residuals. The terminal regions $R_{jm}$ are simply labels that we put on the leaves to keep track of them during each stage of the algorithm.


Note that in real practice decision trees usually have more leaves and sometimes even multiple decision trees are used, but this is simply to illustrate how the process works. In the next part we calculate the output values for each leaf. This is done by doing something similar as in step 1:
\begin{equation}
\begin{align}
& \text{for} \: j = 1, \dots ,J_m: \\
& \text{compute} \: \gamma_{jm} = \underset{\gamma}{\text{argmin}} \sum_{x_i \in R_{jm}}L(y_i, F_{m-1}(x_i) + \gamma).
\end{align}
\end{equation}
The difference from step 1 is that we now include the output of the previous step whereas in step 1 there was no previous step. Furthermore, we do not take the summation over all samples, only the summation over all samples that belong to a specific leaf in the regression tree. Note, given our choice of loss function, the output values will always be the average of the residuals that end up in the same leaf. So taking the two leaves in the figure above we have $\gamma_{1,1} = -17.3$ and $\gamma_{2,1} = (14.7+2.7)/2 = 8.7$.
At last, we simply make a new prediction for each sample using:
\begin{equation}
F_m(x) = F_{m-1}(x) + \nu \sum_{j = 1}^{J_m} \gamma_{jm} I(x \in R_{jm}),
\end{equation}
where $\nu$ is the so-called learning rate and ranges from 0 to 1. Usually, this learning rate is set to a low number to increase the accuracy of the model in the long run. According to Leslie N. Smith from the US Naval Research Laboratory, you could estimate a good learning rate by training the model initially with a very low learning rate and increasing it either linearly or exponentially at each iteration, but this is beyond the scope of this article.
All of this is iterated until stage $M$ of the algorithm. At the last stage, we should get an output value of $F_M(x)$ that has a very low mean squared error and a very accurate prediction for each observation. This is a very detailed description of how gradient boosting works.
XGBoost
eXtreme Gradient Boosting takes gradient boosting even further. It became well known in the machine learning competition circles after its usage in the winning solution of the Higgs Machine Learning Challenge. What makes XGBoost different is that it takes into account a regularization term to avoid overfitting of the model. On the top right of the figure below we see an example of overfitting a model. The best fit is shown in the lower right corner.
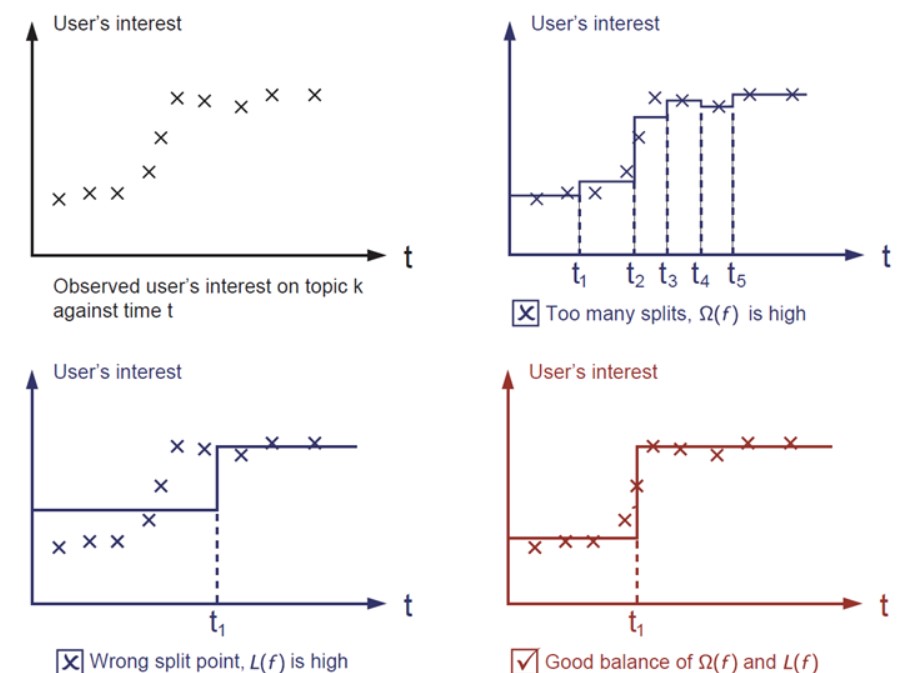
The effect of the regularization term visualized
So in principle, XGBoost is simply gradient boosting but the loss function looks a bit different as it takes into account the possible overfitting unextreme gradient boosting is known to be prone to. It consists of a regularization term that takes into account the output value of the decision trees. This may look like something as follows:
\begin{equation}
\text{Objective function} = \sum_{i=1}^n L(y_i, p_i) + \frac{1}{2}\lambda \sum_{j =1}^T w_j^2,
\end{equation}
where $p_i$ is the prediction of observation $i$ and $w_j$ can be seen as the score on the $j$-th leaf. Furthermore, $T$ is the number of leaves in the decision tree, which the user can set. The last term is the regularization part of our new equation. Now we want to minimize this objective function with respect to the scores of each leaf. I will not show how this is calculated as it is a complicated proof, but for the interested reader you can find it here. From this proof we actually get that the optimal value is:
\begin{equation}
w_j^* = -\frac{g_1 + g_2 + \dots + g_n}{h_1 + h_2 + \dots + h_n + \lambda},
\end{equation}
where $g_i$ is the first derivative of the loss function with respect to $p_i$ and $h_i$ is the second derivative of the loss function with respect to $p_i$. Note that $\lambda$ is a scaling factor that can be set by the user who wants to run the algorithm. The larger the value of $\lambda$, the more emphasis we give on the regularization penalty, which will lead the optimal output value to get closer to 0. This is exactly what regularization is supposed to do.
Noticing that in the formula for $w_j^*$, $g_i$ is simply the negative residual for observation $i$ as we have that our loss function is the MSE. One can show this by simply taking the derivative of $\frac{1}{2}(y_i-p_i)^2$ with respect to $p_i$, which is equal to $-(y_i-p_i)$. This expression is simply the negative residual for the $i$-th observation. Therefore, for $h_i$ we take the derivative of $-(y_i-p_i)$ with respect to $p_i$, which equals to $1$. Hence, we can rewrite $w_j^*$ as follows:
\begin{equation}
w_j^* = \frac{\text{Sum of residuals}}{\text{Number of residuals $+ \lambda$}}.
\end{equation}
This is often called the similarity score and XGBoost uses it to calculate the optimal output value for each leaf in the decision trees. Notice that this is almost exactly the same formula for the output value, $\gamma_{jm}$, used in unexetreme gradient boosting. The only difference here is that we have a regularization paramater $\lambda$ in our denominator.
OLS vs XGBoost
OLS has proved itself to be very useful in finding linear connections in your data. However, with XGBoost this can be done with much more precision, especially when your data set is complex. Nonetheless, the real downside of XGBoost is that it is very prone to overfitting the data. We saw that we can usually solve this by penalizing the regularization term more, but it can still have this issue. In addition, these kinds of boosting models suffer from high estimation variance compared to the linear regression with OLS. This could be due to the fact that we have a rather complex parameter space, whereas OLS has a very simple parameter space.
In addition, OLS is usually more intuitive which makes it a lot more user friendly. Furthemore, OLS gives us an idea of how we should model our data and is very interpretable. So, XGBoost will generally fit training data much better than linear regression, but it is also prone to overfitting and is less easily interpreted. However, boosting algorithms are far more superior to OLS when it comes to high dimensional data, as these algorithms always pick the most relevant variables. Thus, either one may end up being better, depending on your data and your needs. Therefore, you should always check whether the complicated model is actually needed in your case.
References
Chen, T., & Guestrin, C. (2016). XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. PDF
Friedman, J. H. (2002). Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4), 367–378. https://doi.org/10.1016/s0167-9473(01)00065-2
L. N. Smith, “Cyclical Learning Rates for Training Neural Networks,” 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 2017, pp. 464-472, doi: 10.1109/WACV.2017.58. Link
This article is written by Sam Ansari
