Traffic jams are a daily frustration for millions of drivers worldwide. One of the most misunderstood aspects of traffic flow is how to merge efficiently when two lanes come to one. While most drivers believe merging early is the polite and responsible choice, mathematics and traffic engineers prove otherwise. The zipper merge, where drivers use both lanes fully and merge at the last possible moment, is actually the best method for reducing traffic jams and maintaining traffic flow.
Why Do People Resist the Zipper Merge?
Most drivers instinctively merge early when they see a lane closure ahead. They believe this is the “right” thing to do, assuming that drivers who continue in the closing lane until the last second are being aggressive. This belief is based on several biases:
-
The Fairness Principle: Drivers think that merging early is “waiting in line” properly and that late mergers are “cutting” ahead.
-
Social Pressure: If most people merge early, others follow to avoid being seen as rude.
-
Misconception of Safety: Some believe that last-second merging is dangerous, even though studies show it actually reduces sudden accidents.
However, merging early actually leads to longer traffic jams, increased frustration, and lower overall efficiency on the road.
The Science Behind the Zipper Merge
Traffic jams follow patterns based on flow, density, and speed. The key equation for traffic flow is:
Q=k⋅v
Where:
-
Q = flow rate (vehicles per hour)
-
k = density (vehicles per kilometer)
-
v = speed (kilometers per hour)
When drivers merge too early, one lane becomes underused, while the other lane slows down due to jam. This disrupts the balance, reducing speed and overall traffic flow. In contrast, when both lanes are used until the merge point, cars move more smoothly and at a higher average speed.
Another useful concept is queue length reduction, explained by queuing theory:
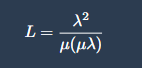
Where:
-
L = queue length
-
λ = arrival rate of cars
-
μ = service rate
In a merging situation, cars arriving at the merge point behave like customers entering a queue. The service rate (μ) represents how quickly cars can pass through the bottleneck, while the arrival rate (λ) represents how fast cars are arriving at the merge point.
-
If λ<μ (arrivals are lower than the service rate), there are no traffic jams.
-
If λ≈μ, minor fluctuations can cause delays.
-
If λ>μ, a traffic jam forms because cars arrive faster than they can merge.
This explains why the way cars merge significantly impacts the length of the queue. Merging early reduces μ (service rate) because traffic slows down. By merging late in a structured, alternating pattern, μ remains high, preventing long congestions.
Final Thoughts
The zipper merge is a perfect example of how math and logic often contradict intuition and social norms. While merging early feels impolite, it actually creates longer queues and worser jams. By contrast, the zipper merge ensures maximum lane usage, smoother transitions, and faster overall travel times.
For drivers, the takeaway is simple: next time you see a merging lane, don’t rush to get over early, but use both lanes until the end and merge fairly, like a zipper. It’s not only smarter but also the best way to keep traffic moving efficiently for everyone